英语
日语
韩语
法语
西班牙语
意大利语
阿拉伯语
葡萄牙语
越南语
俄语
芬兰语
泰语
丹麦语
对外汉语
Parallellinien. Zwei gerade Linien, welche in einerlei Ebene liegen und nach keiner Seite hin1 zusammentreffen, wie weit2 man sie auch verlängert denken mag, heissen parallel (gleichlaufend3).
Wenn man auf dem einen Schenkel eines Winkels gleiche Stücke abschneidet und durch die Teilpunkte Parallele an den andern Schenkel zieht, so schneiden diese auch auf dem andern Schenkel gleiche Stücke ab.
Parallelen zwischen den Schenkeln eines Winkels schneiden auf denselben proportionale Stücke ab.
Zwei Figuren heissen ähnlich, wenn sie gleichwinklig sind und die4 in gleicher Ordnung zwischen gleichen Winkeln liegenden Seiten dasselbe Verhältnis zu einander haben.
In ähnlichen Dreiecken sind die5 den gleichen Winkeln gegenüber liegenden Seiten proportional.
Die Umfänge ähnlicher Figuren verhalten sich6 wie zwei ähnlich liegende Seiten, ihre Inhalte aber wie die Quadrate ähnlich liegender Seiten.
Wenn in einer Proportion die beiden innern Glieder gleich sind, wie in 2:6=6:18, so heisst eines der gleichen mittlern Glieder die mittlere Proportionale oder das geometrische Mittel der beiden äussern.
Das Perpendikel von einem beliebigen Punkte der Peripherie eines Kreises auf den Durchmesser ist die mittlere Proportionale zwischen den beiden Abschnitten des Durchmessers.
Die7 vom Scheitel des rechten Winkels eines rechtwinkligen Dreiecks auf die Hypotenuse gefällte Senkrechte ist das geometrische Mittel zwischen den Abschnitten der Hypotenuse.
Jede der beiden Sehnen ist die mittlere Proportionale[Pg 15] zwischen dem anliegenden8 Abschnitt des Durchmessers und dem ganzen Durchmesser.
Jede Kathete ist das geometrische Mittel zwischen dem anliegenden Abschnitt der Hypotenuse (begrenzt durch die Höhe auf derselben) und der Hypotenuse selbst.
Aufgabe. Ein Quadrat zu zeichnen, welches so gross ist wie ein gegebenes Rechteck; mit anderen Worten, ein gegebenes Rechteck PBDE in ein an Inhalt gleiches Quadrat zu verwandeln.
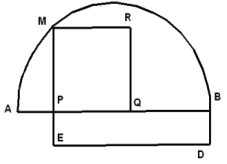
Man füge also PE geradlinig an PB, so dass AP=PE, beschreibe über AB, als Durchmesser, einen Halbkreis, errichte in P auf AB das Perpendikel MP, so ist das über dieses Perpendikel konstruierte Quadrat MPQR das verlangte, weil MP2=AP.PB=PE.PB.
