德国科学阅读：8

Ein Vieleck heisst regelmässig, wenn alle Seiten und alle Winkel gleichgross sind.
 

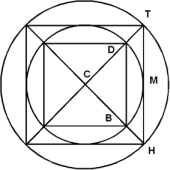
Um um1 einen Kreis ein regelmässiges Viereck zu beschreiben, dessen Seiten mit denen des eingeschriebenen parallel sind, halbiere2 man einen Bogen in M, ziehe durch M eine Tangente, welche die verlängerten Radien CB, CD in T und H schneidet, dann ist HT eine Seite des um[Pg 16]schriebenen Vierecks, welche man nur in dem mit CT als Halbmesser beschriebenen zweiten Kreise herumzutragen3 braucht.

 

Der Inhalt eines4 um den Kreis beschriebenen regelmässigen Vielecks ist gleich der Fläche5 eines Dreiecks, dessen Grundlinie gleich dem Umfang des Vielecks, und dessen Höhe gleich dem halben Radius des Kreises ist.

 

Der Flächeninhalt eines Kreises ist so gross wie der eines Dreiecks, dessen Grundlinie gleich dem Umfange und dessen Höhe gleich dem Halbmesser des Kreises ist.

 

KOERPERLICHE6 GEOMETRIE.

 

So wie man eine gerade Linie nach beiden Enden hin bis in's Unendliche7 verlängert denken kann, so kann man sich auch eine Ebene nach allen Seiten hin bis ins Unendliche ausgedehnt denken.

 

Durch zwei Punkte A und B, oder durch die sie verbindende gerade Linie kann man unzählige Ebenen legen (führen).

 

Körper8 heisst jeder nach allen Richtungen hin begrenzte Raum. Die Summe aller ihn begrenzenden Flächen heisst die Oberfläche des Körpers.

 

Die Linien, in welche sich irgend zwei9 den Körper begrenzende Ebenen schneiden, heissen Kanten.

 

An den Punkten, in welchen drei oder mehrere Grenzebenen zusammenstossen, entsteht10 das, was man, von aussen betrachtet, eine Ecke, von innen gesehen, einen körperlichen Winkel nennt.

 

Jeder Körper, dessen Grundflächen11 kongruente Vielecke, und dessen Seitenflächen, welche die parallelen Seiten dieser Vielecke verbinden, Parallelogramme sind, heisst ein[Pg 17] Prisma, und zwar12 ein dreiseitiges, vierseitiges etc., je nachdem die Grundflächen Dreiecke, Vierecke etc. sind.

 

Walze oder Cylinder (Zylinder) heisst jeder prismatische Körper, der zwei kongruente und parallele Kreise zu Grundflächen hat und dessen Seitenfläche (Mantel) eine einzige solche krumme Fläche ist, deren sämmtliche mit der Grundfläche parallele Durchschnitte der Grundfläche gleich sind.

 

Man unterscheidet gerade und schiefe Cylinder, je nachdem ihre Achse senkrecht oder schief auf der Grundfläche steht.

 

Würfel oder Kubus heisst jedes Parallelopiped, dessen Grundflächen und Seitenflächen Quadrate sind, die folglich gleich und senkrecht auf einander sind.

 

Kegel heisst jeder pyramidische Körper, dessen Grundfläche gewöhnlich ein Kreis, und dessen Seitenfläche (Mantel) eine einzige solche krumme ist, dass darin von der Spitze nach jedem Punkte der Peripherie der Grundfläche eine gerade Linie gezogen werden kann.