德国科学阅读：6

Der Kreis ist eine1 von einer krummen Linie so begrenzte ebene Figur, dass alle ihre Punkte von einem innerhalb liegenden Punkte, den man Mittelpunkt oder Centrum (Zentrum) nennt, gleich weit entfernt sind.

 

Die2 vom Mittelpunkt des Kreises auf eine Sehne3 gefällte Senkrechte halbiert die Sehne und den dazu gehörigen4 Bogen.

 

Aufgabe. Durch 3 ganz beliebig5 gegebene, jedoch nicht in gerader Linie liegende Punkte A, B, C, einen Kreis zu beschreiben.

 

Auflösung. Man verbinde zwei und zwei Punkte AB und BC, so kann man die Linien AB und BC als Sehnen des zu beschreibenden Kreises betrachten. Errichtet man also[Pg 12] auf deren Mittel Perpendikel, so muss jedes derselben durch den gesuchten Mittelpunkt gehen.

 

Der Centriwinkel6 ist immer doppelt so gross als der auf demselben Bogen stehende Peripheriewinkel7.

 

Jeder Winkel im Halbkreise ist ein rechter Winkel.

 

In jedem Parallelogramm sind die gegenüber liegenden Seiten und Winkel einander gleich, und eine Diagonale teilt es in zwei kongruente Dreiecke.

 

Parallelogramme von gleicher Grundlinie und Höhe sind inhaltsgleich.8

 

Der Inhalt eines Dreiecks ist gleich dem halben Produkt aus Grundlinie und Höhe.

 

DER PYTHAGORAEISCHE LEHRSATZ.
 

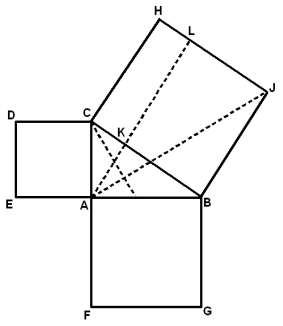
Der Pythagoräische Lehrsatz. In jedem rechtwinkligen Dreieck ist das Quadrat der Hypotenuse so gross wie die Quadrate der beiden Katheten9 zusammengenommen.

 

Beweis. Sei10 CAB ein bei A rechtwinkliges Dreieck,[Pg 13] und seien über seinen drei Seiten Quadrate errichtet, so soll die Fläche des auf der Hypotenuse BC stehenden Quadrats allein so gross sein wie die Flächen der11 beiden auf den Katheten AC und AB stehenden Quadrate zusammengenommen. Aus dem Scheitel A des rechten Winkels sei AL parallel zu CH gezogen, so ist dadurch das Quadrat der Hypotenuse in zwei Rechtecke CHLK und LKBJ geteilt, und es lässt12 sich nun zeigen, dass jedes der beiden Rechtecke seinem benachbarten Quadrate an Inhalt gleich ist. Zieht man nämlich noch die Hülfslinien13 AJ und CG, so haben die beiden Dreiecke ABJ und CBG zwei Seiten und den eingeschlossenen Winkel gleich, nämlich JB=CB.

 

(Man denke sich das Dreieck CBG um den Punkt B gedreht, so fällt der Punkt C auf J und G auf A.)

 

Das Dreieck ABJ hat nun mit dem Rechteck LKBJ einerlei Grundlinie BJ und gleiche Höhe KB; ebenso haben das Dreieck CBG und das Quadrat ABGF einerlei Grundlinie BG und gleiche Höhe AB, daher: △ ABJ=1/2 Rechteck KBJL und CBG=1/2 Quadrat ABGF. Da nun die beiden Dreiecke ABJ und CBG gleich gross sind, so ist auch 1/2 Rechteck KBJL=1/2 Quadrat ABGF, also auch das ganze Rechteck so gross wie das ganze Quadrat.

 

Ebenso zeigt man an der andern Seite, indem man14 die Hülfslinien AH und BD zieht, dass auch das Rechteck CHLK dem Quadrat ACDE an Fläche gleich ist, und folglich auch beide Rechtecke zusammen, d. i.15 das Quadrat der Hypotenuse, so gross ist, wie die Summe der Quadrate der beiden Katheten.

 

Zusatz. Das Quadrat der einen Kathete ist so gross wie das Quadrat der Hypotenuse weniger dem Quadrat der andern Kathete.