德国科学阅读：5. GEOMETRIE.

Eine gerade Linie ist diejenige, welche nicht aus ihrer Lage kommt, wenn sie sich um zwei in ihr liegenden festen Punkte, z. B.1 um ihre Endpunkte, dreht.
 

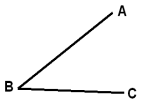
Die2 beiden einen Winkel bildenden Linien BA, BC, heissen die Schenkel, und der Punkt B, in welchem sie zusammenstossen, der Scheitel (der Scheitelpunkt, die Spitze) des Winkels.

 

Zwei Winkel, welche einen Scheitel gemein haben und deren beiden andern Schenkel eine gerade Linie bilden, heissen Nebenwinkel.

 

Alle Winkel, welche an einerlei3 Seite einer geraden Linie liegen und einen Scheitel in derselben gemein haben, betragen zusammen zwei rechte Winkel.

 

Wenn zwei gerade Linien sich schneiden, so sind je zwei gegenüber liegende Winkel, welche man Scheitelwinkel nennt, einander gleich.[Pg 10]

 

Alle Winkel, welche rings um einen gemeinschaftlichen Scheitelpunkt liegen, betragen zusammen immer vier rechte.

 

Zwei Dreiecke sind kongruent4, wenn sie zwei Seiten und den5 von denselben eingeschlossenen Winkel wechselweise gleich haben.

 

Aufgabe. Es6 sind alle drei Seiten, a, b, c, eines Dreiecks gegeben; es soll das dadurch bestimmte Dreieck gezeichnet werden.

 

Auflösung. Man stecke7 eine der gegebenen Seiten, z. B. a in der Linie BC ab, beschreibe aus dem einen Endpunkt B mit der Seite c als Radius einen Bogen mn, ebenso aus C mit der Seite b als Radius einen zweiten Bogen pq, und ziehe von dem Durchschnittspunkt A der beiden Bögen Gerade nach B und C, so ist ABC das verlangte Dreieck.

 

Aufgaben. 1. Auf einer Linie BH in einem bestimmten Punkte D eine Senkrechte zu errichten.

 

2. Eine gegebene Linie zu halbieren.

 

3. Von einem ausserhalb einer Linie GH gegebenen Punkte A eine Senkrechte auf dieselbe zu fällen.

 

Wenn zwei Parallelen von einer dritten Linie geschnitten werden, so entstehen acht Winkel:

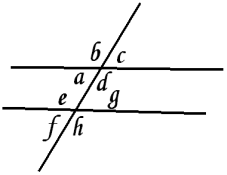
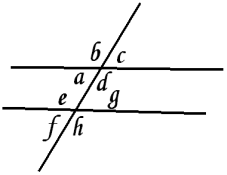
I. Auf einerlei Seite der Schneidenden:

1. Innere Winkel innerhalb der Parallelen.

2. Aeussere Winkel ausserhalb der Parallelen.

3. Korrespondierende oder gleichliegende Winkel (oder[Pg 11] Gegenwinkel) auf einerlei Seite der Parallelen, beide unterhalb oder beide oberhalb.

II. Auf verschiedenen Seiten der Schneidenden:

Wechselwinkel: innere, äussere, korrespondierende.

Wenn zwei Linien gegen eine dritte eine solche Lage haben, dass die inneren Wechselwinkel gleich sind, so sind die Linien parallel.

 

In jedem Dreieck ist die Summe aller Winkel gleich zwei rechten.

 

Ein Dreieck kann also8 nur einen rechten oder nur einen stumpfen Winkel enthalten; die beiden andern müssen alsdann9 spitz sein.

 

Der Aussenwinkel am Dreieck ist gleich der Summe der beiden innern gegenüber liegenden Winkel.

 

Unter Aussenwinkel ist derjenige gemeint, den die Verlängerung einer Seite mit der daran stossenden10 bildet.